الفرنسية: Méthode de la puissance
المبدأ
حدد ![]() و x بحيث Ax =
و x بحيث Ax = ![]() x
x
نفترض أن القيم المميزة لـ A بحيث ![]() (إذن، بالخصوص،
(إذن، بالخصوص، ![]() 1 حقيقي وبسيط).
1 حقيقي وبسيط).
ننشئ متتالية مباشرة، كل منها هي صورة التي سبقتها. المتتالية تقارب الإتجاه المميز المتعلق بـ 1![]() :
:
الخوارزم
لتكن متجهة.
تهيئ: كيفما كان u(0)
تكرار
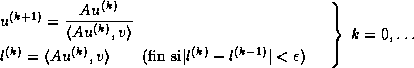
نتيجة:
![]()
![]()
(x1 المتجه المميزة المتعلق بـ 1![]() بحيث
بحيث ![]() )
)
حالة خاصة: v = المتجهة je من القاعدة القانونية ،![]()
تهيئ: كيفما كان u(0)
تكرار:

نتيجة
مثال
أحسب القيمة المميزة لأكبر معيار(ومتجهة المميزة المرتبطة) للمصفوفة:

نختار اعتباطيا متجهة الانطلاقة.

وv لأول متجهة القاعدة القانونية.
الكرتان الأوليتان
(Au(0))1 = (-183)+(53)+(-12)+(28) = -114
(Au(0))2 = (-392)+(113)+(-38)+(65) = -252
(Au(0))3 = (-192)+(56)+(-1)+(25) = -112
(Au(0))4 = (-538)+(157)+(-7)+(71) = -317
l(0) = (Au(0))1 = -114
u(1)1 = 1
u(1)2 = (-252)/(-114) = 126/57
u(1)3 = (-112)/(-114) = 56/57
u(1)4 = (-317)/(-114) = 317/114
(Au(1))1 = (-183)+(53)*(126/57)+(-12)*(56/57)+(28)*(317/114) = 26/114
(Au(1))2 = (-392)+(113)*(126/57)+(-38)*(56/57)+(65)*(317/114) = 137/114
(Au(1))3 = (-192)+(56)*(126/57)+(-1)*(56/57)+(25)*(317/114) = 37/114
(Au(1))4 = (-538)+(157)*(126/57)+(-7)*(56/57)+(71)*(317/114) = -45/114
l(1) = (Au(1))1 = 26/114
u(2)1 = 1
u(2)2 = (137/114)/(26/114) = 137/26
u(2)3 = (37/114)/(26/114) = 37/26
u(2)4 = (-45/114)/(26/114) = -45/26
البرمجة
#include <math.h>
#include <conio.h>
#define NMAX 5
double al_norme_vect(double x[NMAX],int n)
void al_prod_mat_vect(double a[NMAX][NMAX],int n,double x[NMAX],double y[NMAX])
double vp_puissance(double a[NMAX][NMAX],int n,double x[NMAX],double eps)
main()
{
double x[NMAX],r[NMAX];
double a[NMAX][NMAX];
double l1,eps;
int i,j,n;
clrscr();
printf("Méthode de la Puissance\n");
n=4;
a[1][1]=-183;a[1][2]=53;a[1][3]=-12;a[1][4]=28;
a[2][1]=-392;a[2][2]=113;a[2][3]=-38;a[2][4]=65;
a[3][1]=-192;a[3][2]=56;a[3][3]=-1;a[3][4]=25;
a[4][1]=-538;a[4][2]=157;a[4][3]=-7;a[4][4]=71;
printf("Matrice A\n");
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
printf("%12.6e ",a[i][j]);
printf("\n");
}
eps=1e-13;
printf("Les premiers itérés :\n");
for(i=1;i<=n;i++)
x[i]=1;
l1=vp_puissance(a,n,x,eps);
printf("1er couple valeur/vecteur propre (dernier itéré)\n");
printf("lambda1 = %22.16e\n",l1);
printf("x(1) = ");
for(i=1;i<=n;i++)
printf("\n %22.16e ",x[i]);
printf("\n");
al_prod_mat_vect(a,n,x,r);
for(i=1;i<=n;i++)
r[i] -= l1*x[i];
printf("Norme résidu = %.3e\n",al_norme_vect(r,n));
}
نتيجة البرنامج
نحذف التعليقات من الدالة vp_puissance؛ وفي كل كرة البرنامج يظهر :
- المعاد l(k)
- المعادu(k+1)
ثم يظهر بعد ذلك معيار الباقيAx - x
x
مصفوفة A
-1.83000e+02 5.30000e+01 -1.20000e+01 2.80000e+01
-3.92000e+02 1.13000e+02 -3.80000e+01 6.50000e+01
-1.92000e+02 5.60000e+01 -1.00000e+00 2.50000e+01
-5.38000e+02 1.57000e+02 -7.00000e+00 7.10000e+01
Les premiers itérés :
l( 1)=-1.1400e+02 u( 1)=( 1.0000e+00 2.2105e+00 9.8246e-01 2.7807e+00 )
l( 2)= 2.2807e-01 u( 2)=( 1.0000e+00 5.2692e+00 1.4231e+00 -1.7308e+00 )
l( 3)= 3.0731e+01 u( 3)=( 1.0000e+00 1.1990e+00 1.8999e+00 5.0901e+00 )
l( 4)= 2.7159e-01 u( 4)=( 1.0000e+00 7.9124e+00 1.8295e+00 -6.1060e+00 )
l( 5)= 4.3438e+01 u( 5)=( 1.0000e+00 8.2177e-01 2.2243e+00 5.9377e+00 )
l( 10)=-2.2872e-01 u( 10)=( 1.0000e+00 -9.1163e+00 2.3037e+00 2.2607e+01 )
l( 20)=-1.0548e+00 u( 20)=( 1.0000e+00 -1.4301e+00 2.2966e+00 9.7508e+00 )
l( 30)=-1.7893e+00 u( 30)=( 1.0000e+00 -5.5632e-01 2.2964e+00 8.2898e+00 )
l( 40)=-2.3874e+00 u( 40)=( 1.0000e+00 -2.4193e-01 2.2964e+00 7.7641e+00 )
l( 50)=-2.8403e+00 u( 50)=( 1.0000e+00 -9.1986e-02 2.2964e+00 7.5134e+00 )
l( 60)=-3.1646e+00 u( 60)=( 1.0000e+00 -1.0974e-02 2.2964e+00 7.3779e+00 )
l( 70)=-3.3877e+00 u( 70)=( 1.0000e+00 3.5751e-02 2.2964e+00 7.2998e+00 )
l( 80)=-3.5370e+00 u( 80)=( 1.0000e+00 6.3723e-02 2.2964e+00 7.2530e+00 )
l( 90)=-3.6351e+00 u( 90)=( 1.0000e+00 8.0842e-02 2.2964e+00 7.2244e+00 )
l(100)=-3.6986e+00 u(100)=( 1.0000e+00 9.1461e-02 2.2964e+00 7.2066e+00 )
l(110)=-3.7396e+00 u(110)=( 1.0000e+00 9.8103e-02 2.2964e+00 7.1955e+00 )
l(120)=-3.7658e+00 u(120)=( 1.0000e+00 1.0228e-01 2.2964e+00 7.1886e+00 )
l(130)=-3.7825e+00 u(130)=( 1.0000e+00 1.0491e-01 2.2964e+00 7.1842e+00 )
l(140)=-3.7931e+00 u(140)=( 1.0000e+00 1.0658e-01 2.2964e+00 7.1814e+00 )
l(150)=-3.7999e+00 u(150)=( 1.0000e+00 1.0763e-01 2.2964e+00 7.1796e+00 )
أول زوج قيمة /متجهة مميزة(آخر كرة)
lambda1 = -3.811646855751420e+00
x(1) =
1.000000000000000e+00
1.094572319896595e-01
2.296364144307292e+00
7.176553199302955e+00
معيار الباقي= 9.55e-12
الدوال الثانوية
معايير الدالة al_norme_vect هي كالتالي:
x :متجهة (التي فيها نحسب المنظم)
n : بعد المتجهة.
ترجع هذه الدالة المنظم المتجهي الأقليدي (المنظم 2 لـ Holder).
معايير الدالة al_prod_mat_vect هي كالتالي:
a : المصفوفة
n : درجة المصفوفة
x و y : متجهتين
ترجع هذه الدالة في المتجهة y ضرب المصفوفة a في المتجهة x.
الدالة al_prod_matmd_vect
المصفوفة متماثلة قطريا، ومحفوظة في جدول ثنائي البعد بعده NMAX*NDIAG.
معايير الدالة هي كما يلي :
a : مصفوفة متماثلة قطريا ومكدسة
n : درجة المصفوفة
x و y : متجهتين
ترجع هذه الدالة في المتجهة y ضرب المصفوفة a في المتجهة x.
الدالة الرئيسية vp_puissance
معايير هذه الدالة هي كالتالي:
a : المصفوفة
n : درجة المصفوفة
x : جدول أحادي البعد
eps : الدقة المطلوبة
ترجع القيمة المميزة المحسوبة، أما في الجدول x المتجهة المميزة المرتبطة بها.
وهي تستدعي الدالة التالية:
void al_prod_mat_vect(double a[NMAX][NMAX],int n,double x[NMAX],double y[NMAX])
هذه الدالة يجب أن تعرف في البرنامج الرئيسي.
الثابنة الصحيحة NMAX تساوي البعد القصوي للمصفوفة (+1).
double vp_puissance(double a[NMAX][NMAX],int n,double x[NMAX],double eps)
{
int i,j,c;
/* int k; */
double l,l1;
double y[NMAX];
l=0.0;
/* k=1; */
do
{
c=1;
l1=l;
al_prod_mat_vect(a,n,x,y);
while(y[c]==0)c++;
l=y[c];
for(i=1;i<=n;i++)
x[i]=y[i]/ l;
/* if((k<=5)||(k/10*10==k)&&(k<=150))
{
printf("l(%3d)=%11.5e u(%3d)=(",k,l,k);
for(i=1;i<=n;i++)
printf("%11.5e ",x[i]);
printf(")\n");
}
k++; */
}
while (fabs(l-l1)>eps);
return(l);
}
Remarque : si on veut que la fonction affiche quelques itérés, il suffit de supprimer les marques de commentaires /* et */.

