مصطلحات

العربية: التقريب في اتجاه صغار المربعات

الإنجليزية: The method of least squares

الفرنسية: Méthode des moindres carrés 

الحالة العامة

تقريب الدالة f بدالة أخرى g.

لتكن u₀, u₁, ... u_n, n+1 عناصر فضاء متجهي V، مستقل خطيا، E فضاء متجهي من V مولد بمتجهاته، وf V 

 أحسن تقريب لـ f على هو E

a_i حلول النظمة الخطية،

التقريب الحدودي المتقطع

نعتبر الأفاصيل x_i , i = 0,... p. ودالة f(x_i) = y_i بحيث _{i = 0,... p}

نريد تقريب المجموعة المتقطعة لنقط (x_i, y_i) بحدودية من الدرجة n :

P_n(x) = a₀ xⁿ + a₁ x^n-1 + ... a_n-1 x + a_n

ومنه

u₀ = xⁿ, u₁ = x^n-1, ... u_n-1 = x, u_n = 1

(E فضاء ألمتجهي لحدوديات من الدرجة  n )

الجداء السلمي معرف بـ :

a_i حلول النظمة الخطية

=

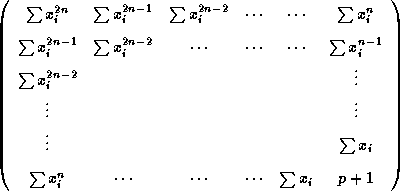
(حالة n = 1)

مثال

نعتبر الدالة f(x) = x² + 2x  على [-1, +1]

احسب قيمة f  في نقط ذات الأفاصيل -1, -1/2, 0, 1/2, 1, ، وحدد مستقيم أحسن تقريب متقطع لـ f بالنسبة لهذه النقط في اتجاه صغار المربعات.

P₁(x) = a₀x + a₁           p = 4

النظمة الخطية

=

=

حلول النظمة

a₀ = 2,  a₁ = 1/2

P₁(x) = 2x + 1/2

التقريب الحدودي المتصل

نريد التقريب على مجال [a, b] دالة f بحدودية من الدرجة n

P_n(x) = a₀ xⁿ + a₁ x^n-1 + ... a_n-1 x + a_n

ومنه

u₀ = xⁿ, u₁ = x^n-1, ... u_n-1 = x, u_n = 1                

(E الفضاء المتجهي لحدوديات من الدرجة  n )

الجداء السلمي معرف بـ

    (  w(x)  دالة الوزن)

مثال

نعتبرالدالة f(x) = x² + 2x  على [-1, +1]

حدد أحسن تقريب متصل لـ f على المجال في إتجاه  صغار المربعات، ونعتبر الجداء المتجهي.

النظمة الخطية

P₁(x) = a₀x + a₁

حلول النظمة

=

=

التقريب المثلثي

a₀ = 2, a₁ = 1/3

P₁(x) = 2x + 1/3

مثل التقريب الحدودي، الحدودية المثلثية ذات درجة n معرفة كما يلي

ومنه

في حالة التقريب المتصل، الجداء المتجهي معرفة بـ:

مثال

نعتبر الدالة f(x) = x² - 2x + 2 على [0, 2].

حدد أحسن تقريب مثلثية لـ f على المجال في اتجاه صغار المربعات، ذي الصيغة

S(x) = a₀/2 + a₁ cos x + b₁ sin x

النظمة الخطية

=

=

حلول النظمة

a₀ = 4(1 -/3),   a₁ = 4,  b₁ = 0
S(x) = 2(1 -/3) + 4 cos x